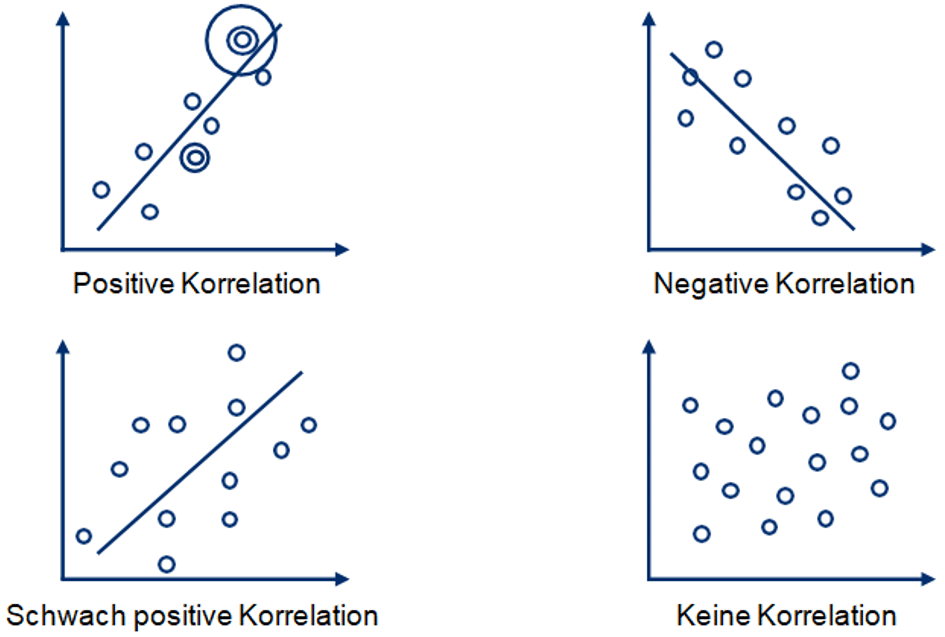
Ein Korrelationsdiagramm zeigt grafisch die Beziehung zwischen zwei paarweise aufgenommenen Merkmalen. Die Merkmale werden im Diagramm als Punkte dargestellt. Aus dieser „Punktwolke“ kann der statistische Zusammenhang zwischen den beiden Merkmalen abgeleitet werden. Zudem lässt sich mit Hilfe des Diagramms die Stärke der Beziehung zwischen zwei Merkmalen ermitteln. Vermutete Ursache-Wirkungs-Beziehungen können so überprüft und schließlich bestätigt oder infrage gestellt werden.
Praktische Anwendung
Vorgehensweise zur Erstellung eines Korrelationsdiagramms:
Beispiel Korrelationsdiagramm
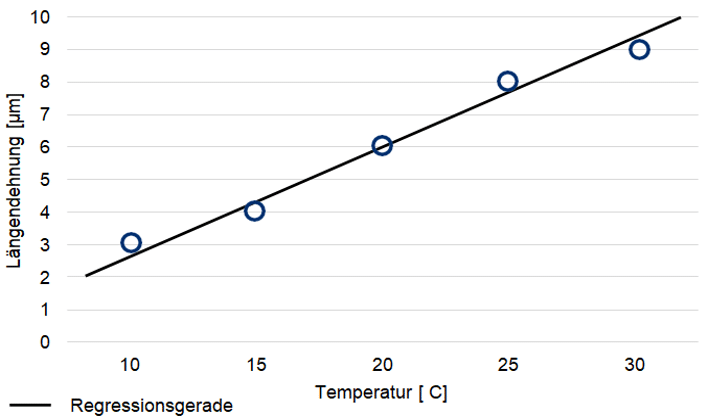
Das Korrelationsdiagramm soll nun anhand eines Beispiels veranschaulicht werden. Untersucht wird der Zusammenhang zwischen der Längendehnung einer Welle zu einem Referenzwert und der Temperatur. Die entsprechenden Werte sind Tabelle zu entnehmen:
| Temparatur [°C] | 10 | 15 | 20 | 25 | 30 |
|---|---|---|---|---|---|
| Längendehnung [µm] | 3 | 4 | 6 | 8 | 9 |
Wie in der Abbildung dargestellt, werden die Wertepaare in das Diagramm eingezeichnet und eine Regressionsgerade durch die Punkte gezogen. Es wird ersichtlich, dass zwischen den Merkmalen eine positive Korrelation besteht. Das heißt, die Längendehnung der Welle steht in direktem Zusammenhang mit der Temperatur.