Qualitätsregelkarte & Histogramm – Werkzeuge der statistischen Prozesskontrolle
Die Qualitätsregelkarte und das Histogramm gehören zu den zentralen Werkzeugen der Statistical Process Control (SPC). Sie ermöglichen es, Prozessschwankungen sichtbar zu machen, Abweichungen frühzeitig zu erkennen und geeignete Korrekturmaßnahmen einzuleiten. Ziel ist die dauerhafte Prozessbeherrschung und die Sicherung gleichbleibender Produktqualität.
Qualitätsregelkarte – Kontrolle der Prozessfähigkeit
Entwickelt von Walter A. Shewhart im Jahr 1931, stellt die Qualitätsregelkarte ein Werkzeug dar, um Prozesse in Echtzeit zu überwachen und Regelabweichungen zu erkennen. Sie ist Teil des Regelkreises im Qualitätsmanagement und bildet das Fundament der SPC.
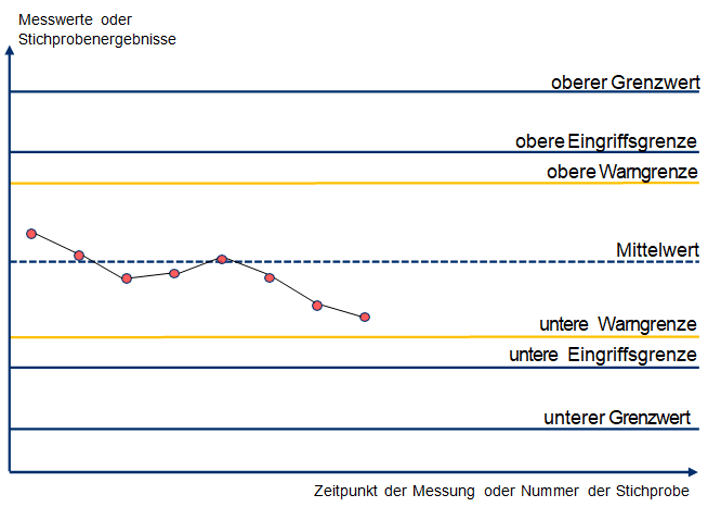
Grafische Darstellung: Qualitätsregelkarte mit Eingriffs- und Warngrenzen
Aufbau und Funktionsweise
Eine Qualitätsregelkarte zeigt Messwerte oder Stichprobenergebnisse über die Zeitachse. Neben dem Mittelwert werden Warngrenzen und Eingriffsgrenzen eingetragen. Überschreitungen signalisieren, dass der Prozess instabil wird und Eingriffe notwendig sind.
Ziel und Nutzen
Qualitätsregelkarten dienen als Frühwarnsystem, um Abweichungen vom Sollzustand rechtzeitig zu erkennen. Sie verhindern Ausschuss, reduzieren Nacharbeit und liefern Anhaltspunkte für Prozessverbesserungen.
Beispielhafte Anwendung
Ein Fertigungsprozess wird regelmäßig überprüft. Zeigen sich Werte außerhalb der Eingriffsgrenzen, muss der Bediener sofort eingreifen. Werden Trends erkannt, kann durch Anpassungen im Prozess (z. B. Werkzeugwechsel) frühzeitig reagiert werden.
Qualitätsregelkreis – Prozesssteuerung im Überblick
Der Qualitätsregelkreis zeigt, wie Regelkarten in einen aktiven Steuerungsprozess eingebunden sind. Er verbindet Sollwerte, Messsysteme und Reaktionsmaßnahmen zu einem geschlossenen Regelprozess.
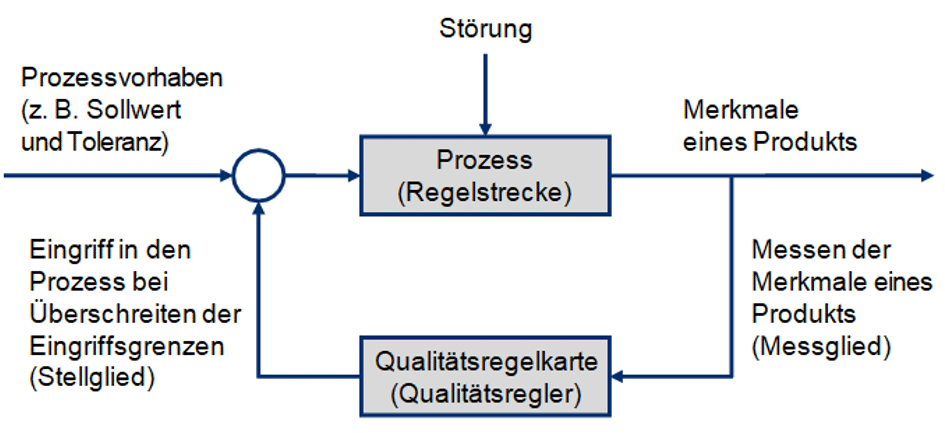
Darstellung: Regelkreis zwischen Prozess, Messung und Eingriff
Histogramm – Darstellung der Prozessstreuung
Das Histogramm zeigt, wie Messwerte innerhalb von Toleranzgrenzen verteilt sind. Es liefert wichtige Informationen zur Streuung und Prozessfähigkeit.

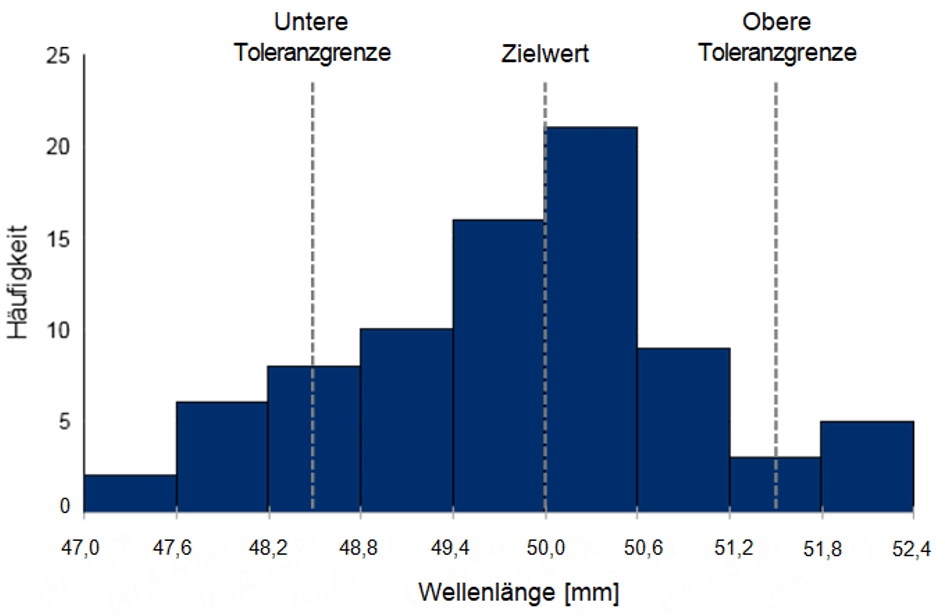
Visualisierung: Häufigkeitsverteilung der Messergebnisse (Histogramm)
Aufbau des Histogramms
Die X-Achse zeigt die Klassen (z. B. Wellenlängenbereiche), während die Y-Achse die Häufigkeit der Messwerte darstellt. Jede Säule symbolisiert, wie viele Teile innerhalb einer bestimmten Klasse liegen – ideal zur Beurteilung der Prozessstreuung.
Beispiel: Vermessung von 80 Wellen
Die Wellen wurden in neun Klassen mit einer Breite von 0,6 mm eingeteilt. Zielwert: 50 mm, Toleranzen: 48,5 mm – 51,5 mm. Die Verteilung zeigt eine symmetrische, aber zu breite Streuung. Ziel der Prozessoptimierung ist es, die Streuung durch präventive Maßnahmen zu reduzieren.
Fazit – Qualitätsregelkarte & Histogramm als Kontrollinstrumente
Qualitätsregelkarten und Histogramme sind unverzichtbare Werkzeuge, um Prozesse transparent, messbar und steuerbar zu machen. Während die Regelkarte Abweichungen in Echtzeit sichtbar macht, liefert das Histogramm eine statistische Übersicht der Prozessfähigkeit. Gemeinsam ermöglichen sie eine fundierte Entscheidungsgrundlage für nachhaltige Qualitätsverbesserungen.
FAQ – Qualitätsregelkarte, Histogramm & Statistische Prozesskontrolle (SPC)
Die statistische Prozesskontrolle (SPC) mit Hilfe von Qualitätsregelkarten und Histogrammen ist ein zentrales Werkzeug zur Prozessüberwachung in der Automobil- und Fertigungsindustrie. Nachfolgend findest du die häufigsten Fragen zu Anwendung, Auswertung und Nutzen dieser Methoden im Rahmen der IATF 16949.
Was ist der Zweck einer Qualitätsregelkarte (Control Chart)?
Eine Qualitätsregelkarte zeigt, wie stabil ein Prozess über die Zeit arbeitet. Sie dient dazu, zufällige Streuungen (allgemeine Ursachen) von systematischen Abweichungen (besondere Ursachen) zu unterscheiden. Wird eine Eingriffsgrenze überschritten, ist der Prozess nicht mehr beherrscht – ein Eingriff ist erforderlich.
Worin unterscheidet sich ein Histogramm von einer Regelkarte?
Ein Histogramm zeigt die Verteilung von Messwerten zu einem Zeitpunkt – also wie häufig bestimmte Werte innerhalb der Toleranz vorkommen. Die Regelkarte dagegen zeigt die Entwicklung der Werte über die Zeit. Beide Methoden ergänzen sich: das Histogramm liefert die statische Momentaufnahme, die Regelkarte das dynamische Prozessverhalten.
Welche Arten von Qualitätsregelkarten gibt es?
Es gibt verschiedene Regelkartentypen – abhängig von den Messdaten:
- X̄-R-Karte: Für Mittelwerte und Spannweiten kleiner Stichproben.
- p-Karte: Für Anteile fehlerhafter Teile in Stichproben.
- u-Karte: Für Fehlerzahlen pro Mengeneinheit (z. B. pro Meter, Stück).
- I-MR-Karte: Für Einzelmesswerte und deren gleitende Unterschiede.
Die Auswahl richtet sich nach Art, Größe und Frequenz der Messungen.
Was bedeuten Warngrenzen und Eingriffsgrenzen?
Die Warngrenzen markieren den Bereich, in dem eine Beobachtung erforderlich ist – der Prozess zeigt erste Anzeichen einer Unregelmäßigkeit. Werden Eingriffsgrenzen überschritten, ist ein sofortiges Eingreifen notwendig, da der Prozess außer Kontrolle geraten ist. Diese Grenzen liegen in der Regel bei ±3 σ (Sigma) um den Mittelwert.
Was versteht man unter Cp und Cpk in der Prozessfähigkeit?
Cp beschreibt die potenzielle Prozessfähigkeit – also, wie breit die Toleranz im Verhältnis zur tatsächlichen Prozessstreuung ist. Cpk hingegen bewertet die tatsächliche Prozesslage und berücksichtigt, ob der Mittelwert verschoben ist. Werte über 1,33 gelten als stabil und beherrscht; unter 1,0 als kritisch.
Wann sollte SPC eingeführt werden?
SPC ist besonders sinnvoll bei stabilen, wiederkehrenden Prozessen mit hoher Stückzahl, beispielsweise in Serienfertigungen. In Entwicklungsphasen oder bei Kleinserien sollte SPC erst nach Prozessvalidierung eingesetzt werden, da statistische Werte sonst zu stark schwanken.
Wie unterstützt SPC die Anforderungen der IATF 16949?
Die IATF 16949 fordert die Anwendung statistischer Methoden zur Prozessüberwachung und Lenkung (Kapitel 9.1.1.1). SPC liefert dabei den Nachweis einer prozessfähigen, beherrschten Produktion – eine Voraussetzung für Serienfreigaben, Kundenabnahmen und die Auditkonformität nach VDA 6.3.
Interne Verlinkungen zu QM Methoden und Werkzeugen
Weiterführende Inhalte auf smct management
Systematische Erfassung von Fehlerarten als Grundlage für Analysen und Verbesserungen.
Werkzeug der statistischen Prozesslenkung zur Überwachung und Steuerung von Prozessen.
Priorisierung von Fehlern und Ursachen nach dem grössten Einfluss auf Qualität und Kosten.
Darstellung von Zusammenhängen zwischen zwei Merkmalen zur Ursachenanalyse.
Qualitätssicherung und Qualitätskontrolle
Vorbeugende Qualitätssicherung und produktbezogene Kontrolle als Basis stabiler Prozesse.
Ursachenanalyse nach Kategorien wie Mensch, Maschine, Material und Methode.
Six Sigma Methode und 9999966 Prozent
Datenbasierter Ansatz zur Reduzierung von Fehlern und Schwankungen in Prozessen.
Ursachenfindung durch wiederholtes Fragen nach dem Grund eines Problems.
Strukturierte Werkzeuge zur nachhaltigen Beseitigung von Fehlern und Störungen.
Kompakte Problemlösung auf einer Seite nach dem Toyota Prinzip mit Fokus auf Ursachen und Massnahmen.
Korrektur und Vorbeugungsmassnahmen in der ISO 9001
Anforderungen an die wirksame Behandlung von Abweichungen, deren Ursachen und die Bewertung der Wirksamkeit von Massnahmen.
Qualität und kontinuierlicher Verbesserungsprozess
Methoden und Vorgehensweisen für nachhaltige Verbesserungen in Prozessen und Abläufen.
Beschwerdemanagement in Unternehmen
Bedeutung einer strukturierten Reklamationsbearbeitung für Kundenzufriedenheit und kontinuierliche Verbesserung.
