📊 Pareto-Analyse – Konzentration auf das Wesentliche
Die Pareto-Analyse ist ein zentrales Werkzeug im Qualitätsmanagement und in der Prozessoptimierung. Sie beruht auf dem sogenannten 80/20-Prinzip: Etwa 80 % der Auswirkungen eines Problems lassen sich meist auf 20 % der Ursachen zurückführen. Durch ihre Anwendung können Unternehmen die Hauptfehlerquellen identifizieren und ihre Ressourcen gezielt auf die größten Verbesserungspotenziale konzentrieren.
📈 Ziel und Funktionsweise der Pareto-Analyse
Ziel der Pareto-Analyse ist die Priorisierung von Fehlern, Ursachen oder Problemen nach ihrer Bedeutung. Sie hilft, die entscheidenden Einflussfaktoren zu erkennen, die den größten Effekt auf Qualität, Kosten oder Effizienz haben.
🎯 Kernaussage des Pareto-Prinzips
Das Pareto-Prinzip – benannt nach dem italienischen Ökonomen Vilfredo Pareto – beschreibt, dass ein kleiner Anteil der Ursachen (rund 20 %) meist den größten Teil der Wirkung (rund 80 %) ausmacht. Dieses Prinzip dient als Grundlage für die Priorisierung in der Qualitätsverbesserung.
📋 Anwendung im Qualitätsmanagement
Im Qualitätsmanagement wird die Pareto-Analyse genutzt, um die häufigsten oder kostenintensivsten Fehlerarten zu identifizieren. Durch ihre Anwendung können Prozesse gezielt verbessert und Fehlerquellen effizient beseitigt werden – beispielsweise in der Produktion, Montage oder im Kundendienst.
🧠 Praktische Anwendung der Pareto-Analyse
Die Erstellung eines Pareto-Diagramms folgt einer klaren und systematischen Vorgehensweise. Dabei werden die Fehlerarten nach Häufigkeit oder Kosten priorisiert und grafisch dargestellt.
🔹 Schritt 1: Definition der Fehlerarten
Erfassen Sie potenzielle Fehler oder Ursachen und kategorisieren Sie diese nach Gemeinsamkeiten. Eine klare Abgrenzung der Kategorien verhindert doppelte Zählungen und erhöht die Aussagekraft der Analyse.
🔹 Schritt 2: Datenerfassung und Sortierung
Sammeln Sie Mess- oder Prüfdaten, zählen Sie die Häufigkeit der Fehler und ordnen Sie sie nach abnehmender Bedeutung. Alternativ können auch Kosten oder Reklamationsaufwände als Bewertungskriterium herangezogen werden.
🔹 Schritt 3: Grafische Darstellung
In einem Pareto-Diagramm werden die Fehlerarten als Balken in absteigender Reihenfolge dargestellt. Zusätzlich wird die kumulierte Summe der relativen Häufigkeiten als Linie eingezeichnet – so erkennt man den Anteil der Hauptursachen auf einen Blick.
🔹 Schritt 4: Ableitung von Maßnahmen
Basierend auf der Analyse können gezielte Maßnahmen zur Fehlervermeidung und Kostenreduktion definiert werden. Häufig konzentriert sich die Optimierung auf die oberen 20–30 % der Fehlerarten, da diese den größten Effekt auf Qualität und Effizienz haben.
📊 Beispiel: Pareto-Analyse in der Endprüfung
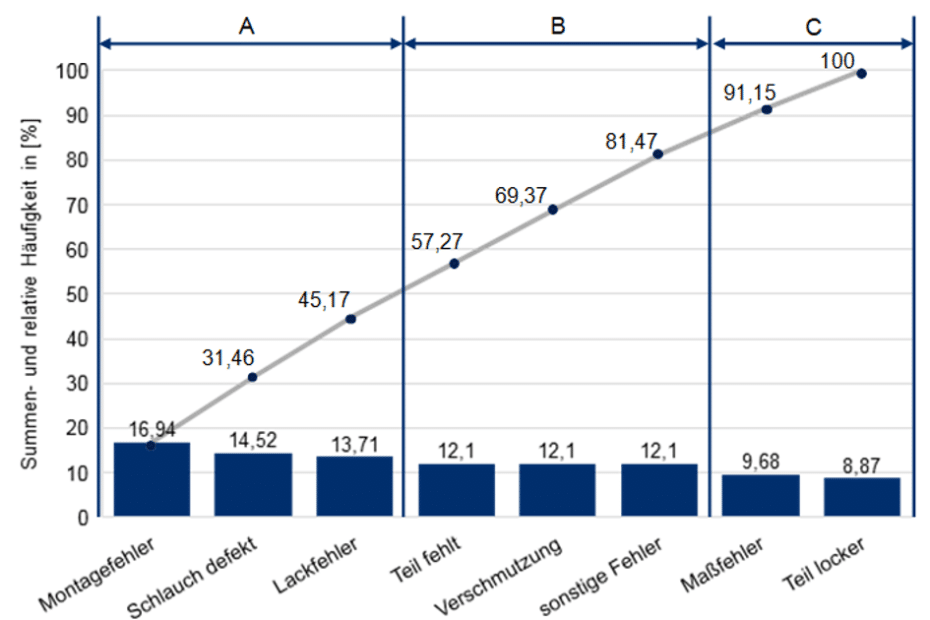
In einer Endprüfung wurden acht verschiedene Fehlerarten erfasst und nach Häufigkeit analysiert. Das Ergebnis zeigt, dass wenige Fehlerarten (Klasse A) den größten Anteil aller Fehler ausmachen.
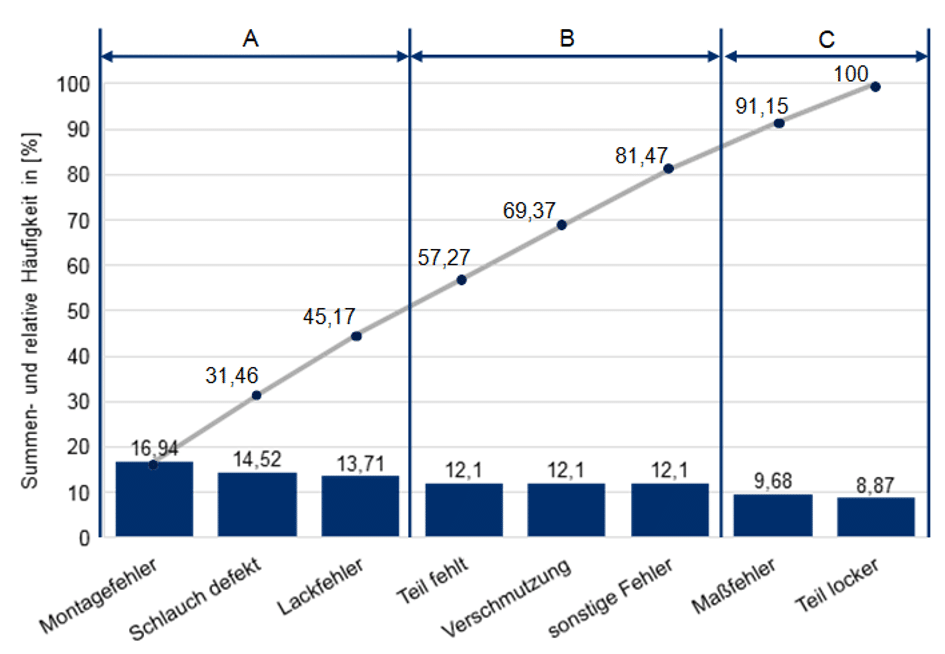
Beispieldarstellung: Pareto-Diagramm mit Fehlerklassen A, B und C
🔹 Interpretation der Ergebnisse
Die ersten drei Fehlerarten verursachen etwa 45 % aller Fehler (Klasse A) – hier ist das größte Verbesserungspotenzial vorhanden. Klasse B umfasst 36 %, Klasse C die restlichen 19 %. Diese Einteilung ermöglicht eine strukturierte Priorisierung für Fehleranalysen und Maßnahmenpläne.
📋 Tabelle – Fehleranalyse nach Pareto-Prinzip
Die folgende Tabelle zeigt die häufigsten Fehlerarten mit relativer Häufigkeit, Summenhäufigkeit sowie den wirtschaftlichen Auswirkungen durch Nacharbeitskosten.
| Fehlerart | Anzahl | rel. Häufigkeit (%) | Summenhäufigkeit (%) | Nacharbeitskosten (€) | Gesamtkosten (€) |
|---|---|---|---|---|---|
| Montagefehler | 21 | 16,94 | 16,94 | 28,50 | 4,83 |
| Schlauch defekt | 18 | 14,52 | 31,46 | 7,00 | 1,02 |
| Lackfehler | 17 | 13,71 | 45,17 | 49,50 | 6,79 |
| Teil fehlt | 15 | 12,10 | 57,27 | 16,50 | 2,00 |
| Verschmutzung | 15 | 12,10 | 69,37 | 12,50 | 1,51 |
| Sonstige Fehler | 15 | 12,10 | 81,47 | 8,50 | 1,03 |
| Maßfehler | 12 | 9,68 | 91,15 | 13,00 | 1,26 |
| Teil locker | 11 | 8,87 | 100,00 | 9,50 | 0,84 |
Die Tabelle zeigt, dass insbesondere Montagefehler, Lackfehler und Schlauchdefekte die größten Kostentreiber darstellen. Sie bilden die Prioritätenklasse A in der Pareto-Analyse und sollten vorrangig verbessert werden.
💶 Erweiterung: Ökonomische Betrachtung
Neben der Fehlerhäufigkeit kann auch die Kostenwirkung bewertet werden. Hierzu werden die Nacharbeitskosten je Fehlerart mit der relativen Häufigkeit multipliziert. Das Ergebnis zeigt häufig größere Unterschiede als die reine Fehlerbetrachtung und verdeutlicht, wo wirtschaftliche Einsparungen am effektivsten erzielt werden können.
✅ Fazit – Pareto-Analyse als Entscheidungshilfe
Die Pareto-Analyse ist ein einfaches, aber äußerst wirkungsvolles Werkzeug, um sich auf die entscheidenden Probleme zu konzentrieren. Sie liefert eine klare Handlungspriorisierung und schafft Transparenz in komplexen Fehlerlandschaften. In Kombination mit Methoden wie der Fehlersammelkarte oder der FMEA bildet sie eine Grundlage für ein effektives Qualitätsmanagement nach ISO 9001 und IATF 16949.
❓ FAQ – Pareto-Analyse im Qualitätsmanagement
Die Pareto-Analyse ist ein einfaches, aber äußerst wirksames Werkzeug im Qualitätsmanagement. Sie hilft, den Fokus auf die wichtigsten Probleme zu richten – also auf die Ursachen, die den größten Einfluss haben. Nachfolgend findest du häufig gestellte Fragen zur Anwendung, Interpretation und Integration der Methode nach ISO 9001 und IATF 16949.
🔹 Was ist das Ziel der Pareto-Analyse?
Ziel der Pareto-Analyse ist es, die wesentlichen Einflussfaktoren auf ein Problem oder eine Abweichung zu identifizieren. Das zugrunde liegende 80/20-Prinzip besagt, dass rund 80 % der Auswirkungen durch nur 20 % der Ursachen entstehen. Damit können Unternehmen gezielt dort ansetzen, wo der größte Nutzen entsteht.
🔹 Wie unterscheidet sich die Pareto-Analyse von anderen QM-Methoden?
Die Pareto-Analyse ist ein Priorisierungswerkzeug. Sie zeigt, welche Fehlerarten oder Ursachen den größten Anteil am Gesamtproblem haben – im Gegensatz zu Methoden wie der FMEA, die Ursachen systematisch analysiert, oder der Fehlersammelkarte, die Daten zunächst sammelt. Pareto ist der logische nächste Schritt zur Fokussierung von Verbesserungsmaßnahmen.
🔹 Wann sollte eine Pareto-Analyse durchgeführt werden?
Immer dann, wenn mehrere Ursachen oder Fehlerarten gleichzeitig auftreten und Ressourcen gezielt eingesetzt werden sollen. Typische Einsatzbereiche sind:
- 📦 Fehleranalyse in Produktion und Montage
- 📊 Reklamationsauswertung und Kostenanalyse
- 🧠 Ursachenanalyse im Rahmen von KVP-Workshops
- 🔧 Priorisierung von Maßnahmen im Problemlösungsprozess (z. B. 8D-Report)
🔹 Wie interpretiere ich ein Pareto-Diagramm richtig?
Im Pareto-Diagramm werden Fehlerarten (x-Achse) nach Häufigkeit sortiert dargestellt, während die y-Achse den kumulierten Anteil zeigt. Die steil ansteigende Kurve kennzeichnet die Hauptursachen. Diese ersten 20–30 % der Ursachen verursachen meist den Großteil der Probleme – und sollten daher vorrangig analysiert und bearbeitet werden.
🔹 Wie oft sollte eine Pareto-Analyse durchgeführt werden?
Eine Pareto-Analyse sollte regelmäßig erfolgen – beispielsweise monatlich oder nach Abschluss einer Serienphase. Bei stark schwankenden Prozessen empfiehlt sich eine laufende Aktualisierung, um Trends frühzeitig zu erkennen und Maßnahmen kontinuierlich zu bewerten.
🔹 Was sind die Klassen A, B und C in der Pareto-Analyse?
Die Einteilung in A-, B- und C-Klassen erfolgt zur besseren Priorisierung von Fehlerarten:
- Klasse A: Die wichtigsten Ursachen – meist 20 % der Fehler, die 70–80 % der Auswirkungen verursachen.
- Klasse B: Mittlere Ursachen mit moderatem Einfluss – ca. 15–25 % der Probleme.
- Klasse C: Geringe Ursachen mit wenig Einfluss – Analyse meist nachrangig.
Diese Kategorisierung dient als Grundlage für Ressourcenplanung und Priorisierung von KVP-Maßnahmen.
🔹 Wie lässt sich die Pareto-Analyse mit anderen QM-Tools kombinieren?
Die Pareto-Analyse wird häufig in Kombination mit anderen Methoden eingesetzt:
- 📋 Fehlersammelkarte: Basisdatenerfassung für die Analyse.
- ⚙️ FMEA: Detaillierte Ursachenbewertung der Hauptfehler (Klasse A).
- 📈 SPC: Statistische Überwachung der relevanten Prozesse.
- 🧭 KVP/8D-Report: Umsetzung und Nachverfolgung der Verbesserungsmaßnahmen.
So entsteht eine durchgängige, faktenbasierte Prozessoptimierung.
